Trójkąt równoboczny

(ang: equilateral triangle)

Aby narysować trójkąt równoboczny należy powtórzyć trzy razy: narysuj bok, skręć w prawo (lub lewo) o 120 stopni.

Podczas rysowania żółw w sumie wykonuje obrót o 360 stopni a ponieważ robi 3 skręty więc każdy z nich ma 360/3 = 120 stopni.

import turtle

turtle.forward(300)
turtle.left(120)

turtle.forward(300)
turtle.left(120)

turtle.forward(300)
turtle.left(120)

turtle.mainloop()

W powyższym kodzie ostatni skręt w lewo właściwie nie jest potrzebny ale dzięki niemu na koniec rysowania żółw jest zwrócony w tą samą stronę jak był przed rysowaniem. Ułatwia to planowanie kolejnej figury.

Z powyższego widać też, że można to łatwo zapisać z użyciem for.

import turtle

for _ in range(3):
    turtle.forward(300)
    turtle.left(120)

turtle.mainloop()

UWAGA: W kodzie używam for _ in ... zamiast for x in ... ponieważ ta wartość (x) nie jest mi potrzebna wewnątrz pętli. Dzięki _ nie muszę wymyślać nowej zmiennej tak aby przypadkiem nie nadpisać zawartości już istniejącej zmiennej (zwłaszcza w dłuższym kodzie). Zmienna _ jest też taką zwyczajową zmienną dla pokazania innym, że ta wartość nie będzie mi niepotrzebna w pętli.

Jak widać, podczas takiego rysowania nie trzeba wyliczać pozycji wierchołków (korzystając z siniusa i cosinusa lub z twierdzenia Pitagorasa). turtle pozwala jednak zobaczyć współrzędne wierzchołków (pozycję żółwia) za pomocą turtle.pos(). Może to być przydatne w pewnych sytuacjach.

import turtle

for _ in range(3):
    print(turtle.pos())
    turtle.forward(300)
    turtle.left(120)

turtle.mainloop()

(0.00,0.00)
(300.00,0.00)
(150.00,259.81)

Można z tego kodu zrobić funkcję aby narysować wiele trójkątów - np. różnej wielkości.

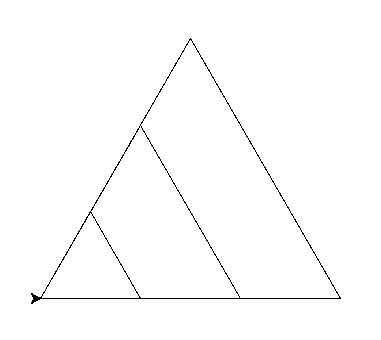
import turtle

def trojkat_rownoboczny(bok)
    for _ in range(3):
        turtle.forward(bok)
        turtle.left(120)

trojkat_rownoboczny(100)
trojkat_rownoboczny(200)
trojkat_rownoboczny(300)

turtle.mainloop()

Można to zrobić także z użyciem petli for

import turtle

def trojkat_rownoboczny(bok)
    for _ in range(3):
        turtle.forward(bok)
        turtle.left(120)

for x in range(1, 4):
    trojkat_rownoboczny(x*100)

turtle.mainloop()

lub wykorzystując możliwości range(początek, koniec, krok) pamiętając, że koniec nie wchodzi w zakres zwracanych wartości więc jeśli chcemy otrzymać 300 to koniec musi być 301 (lub większy)

import turtle

def trojkat_rownoboczny(bok)
    for _ in range(3):
        turtle.forward(bok)
        turtle.left(120)

for bok in range(100, 301, 100):
    trojkat_rownoboczny(bok)

turtle.mainloop()

Można oczywiście zastosować też listę (lub tuplę/krotkę) zamiast range() i wtedy wartości mogą być bardziej "losowe"

import turtle

def trojkat_rownoboczny(bok)
    for _ in range(3):
        turtle.forward(bok)
        turtle.left(120)

for bok in [100, 200, 300]:
    trojkat_rownoboczny(bok)

turtle.mainloop()

Jak widać użycie for pozwala więc łatwo zmieniać ilość.

---

Zamiast zmieniać wielkość trójkąta można też obracać żółwia przed narysowanie każdej z figur.

import turtle

def trojkat_rownoboczny(bok)
    for _ in range(3):
        turtle.forward(bok)
        turtle.left(120)

trojkat_rownoboczny(100)
turtle.left(120)
trojkat_rownoboczny(100)
turtle.left(120)
trojkat_rownoboczny(100)
turtle.left(120)

turtle.mainloop()

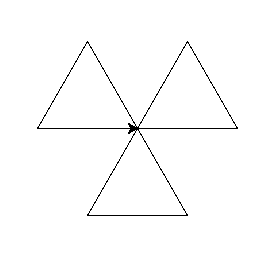
Tu ponownie widać, że kod się powtarza więc można zastosować pętlę for

import turtle

def trojkat_rownoboczny(bok):
    for _ in range(3):
        turtle.forward(bok)
        turtle.left(120)

for _ in range(3):
    trojkat_rownoboczny(100)
    turtle.left(120)

turtle.mainloop()

Można też zmienić ilość powtórzeń i automatycznie wyliczać kąt

import turtle

def trojkat_rownoboczny(bok):
    for _ in range(3):
        turtle.forward(bok)
        turtle.left(120)

bok = 100
ilosc = 4
kat = 360/ilosc

for _ in range(ilosc):
    trojkat_rownoboczny(bok)
    turtle.left(kat)

turtle.mainloop()

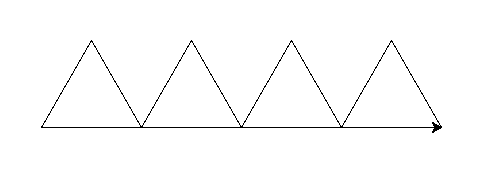
Zamiast zmieniać kąt można też przesuwać żółwia przed narysowaniem kolejnego trójkąta.

import turtle

def trojkat_rownoboczny(bok):
    for _ in range(3):
        turtle.forward(bok)
        turtle.left(120)

bok = 100
ilosc = 4

for _ in range(ilosc):
    trojkat_rownoboczny(bok)
    turtle.forward(bok)

turtle.mainloop()

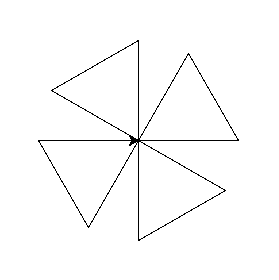
Można też połączyć przesuwanie i skręcanie w prawo

import turtle

def trojkat_rownoboczny(bok):
    for _ in range(3):
        turtle.forward(bok)
        turtle.left(120)

bok = 100
ilosc = 4
kat = 360/ilosc

for _ in range(ilosc):
    trojkat_rownoboczny(bok)
    turtle.forward(bok)
    turtle.right(kat)

turtle.mainloop()

ilosc = 4

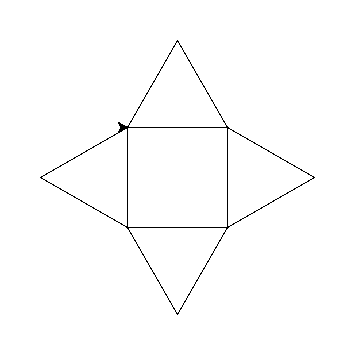
ilosc = 5

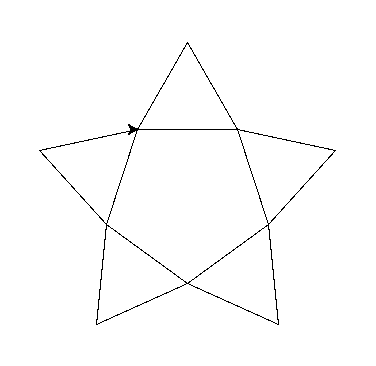
Można też skręcać w lewo

import turtle

def trojkat_rownoboczny(bok):
    for _ in range(3):
        turtle.forward(bok)
        turtle.left(120)


bok = 100
ilosc = 5
kat = 360/ilosc

for _ in range(ilosc):
    trojkat_rownoboczny(bok)
    turtle.forward(bok)
    turtle.left(kat)

turtle.mainloop()

ilosc = 5

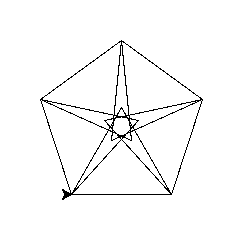
ilosc = 10

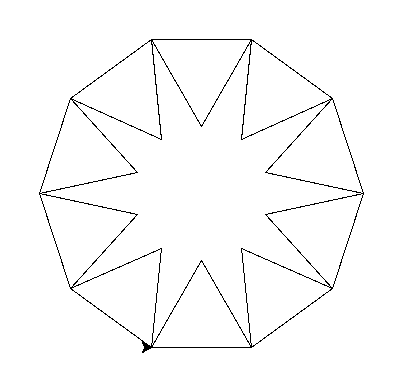
Pod dodaniu kreski do trójkąt mamy flagę

import turtle

def trojkat_rownoboczny(bok):
    for _ in range(3):
        turtle.forward(bok)
        turtle.right(120)

def flaga(bok, ):
    turtle.forward(100)      # narysuj patyk
    trojkat_rownoboczny(bok) # narysuj trójkąt flagi
    turtle.backward(100)     # wycofaj się na początkowe miejsce

ilosc = 12
kat = 360/ilosc

for _ in range(ilosc):
    flaga(50)
    turtle.left(kat)

turtle.mainloop()

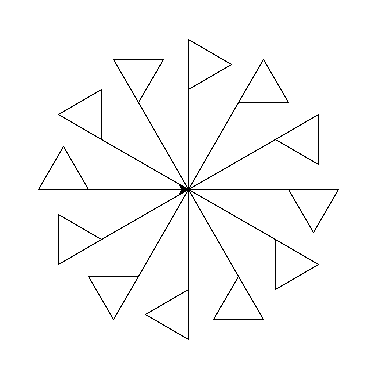
Można też zmieniać wielkość flagi

import turtle

def trojkat_rownoboczny(bok):
    for _ in range(3):
        turtle.forward(bok)
        turtle.right(120)

def flaga(bok, ):
    turtle.forward(100)      # narysuj tyczkę
    trojkat_rownoboczny(bok) # narysuj trójkąt flagi
    turtle.backward(100)     # wycofaj się na początkowe miejsce

ilosc = 12
kat = 360/ilosc

for x in range(ilosc):
    flaga(10 * x)
    turtle.left(kat)

turtle.mainloop()

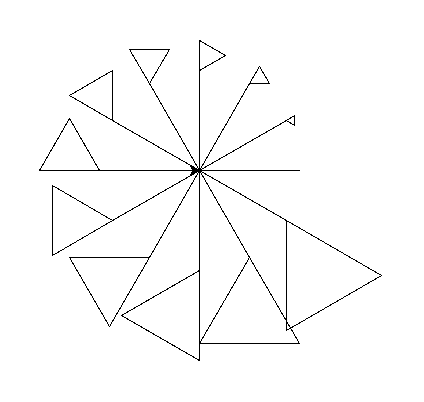
itd.

Trójkąt prostokątny i inne

(ang: rectangular triangle)

Aby narysować trójkąt z turtle należy znać długości trzech boków i wszystkie katy między nimi - a właściwie ich dopełnienie do 180 stopni.

turtle.forward(bok_a)
turtle.left(180 - kat_miedzy_a_b)

turtle.forward(bok_b)
turtle.left(180 - kat_miedzy_b_c)

turtle.forward(bok_c)
turtle.left(180 - kat_miedzy_c_a)

Jeśli mamy trójkąt prostokątny, dla którego znamy tylko boki a i b (czyli te koło kąta prostego) i kąt między nimi (czyli 90 stopni) to bok c możemy wyliczyć z twierdzenia Pitagorasa ( a**2 + b**2 = c**2 czyli c = math.sqrt(a**2 + b**2) ) a kąty między bokami a i c oraz bokami b i c za pomocą arcus tangensa <https://pl.wikipedia.org/wiki/Funkcje_cyklometryczne>'__) (funkcji odwrotnej do tangensa), która jest dostępny jako `math.atan.

a/b i b/a to tangensy odpowiednich kątów, math.atan() zamienia tangensy na kąty w radianach, a math.degrees() zamienia radiany na stopnie.

import turtle
import math

a = 100
b = 150
kat_a_b = 90

c = math.sqrt(a**2 + b**2)

kat_b_c = math.degrees(math.atan(a/b))
kat_c_a = math.degrees(math.atan(b/a))

turtle.forward(a)
turtle.left(180 - kat_a_b)

turtle.forward(b)
turtle.left(180 - kat_b_c)

turtle.forward(c)
turtle.left(180 - kat_c_a)

turtle.mainloop()

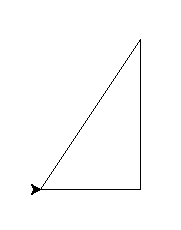
i to samo jako funkcja

import turtle
import math

def trojkat_prostokatny(a, b, kat):

    c = math.sqrt(a**2 + b**2)

    kat_a_b = kat
    kat_b_c = math.degrees(math.atan(a/b))
    kat_c_a = math.degrees(math.atan(b/a))

    turtle.forward(a)
    turtle.left(180 - kat_a_b)

    turtle.forward(b)
    turtle.left(180 - kat_b_c)

    turtle.forward(c)
    turtle.left(180 - kat_c_a)


trojkat_prostokatny(100, 150)

turtle.mainloop()

Te wszystkie obliczenia można jednak obejść wykorzystując turtle.position() do zapamiętania pozycji pierwszego wierzchołka i turtle.goto() do przejścia z ostatniego wierzchołka wprost do pierwszego.

Na koniec zostaje tylko obrócić głowę żółwia w pierwotnym kierunku - ale to już nie stanowi problemu.

import turtle

a = 100
b = 150
kat = 90

pos = turtle.position()  # zapamiętanie pierwszego wierzchołka

turtle.forward(a)        # pierwszy bok
turtle.left(180 - kat)
turtle.forward(b)        # drugi bok

turtle.goto(pos)         # skok do pierwszego wierzchołka i rysowanie trzeciego boku

turtle.right(180 - kat)  # przywrócenie pierwotnego kierunku głowy żółwia

turtle.mainloop()

Ta metoda ma tą zaletę, że pozwala rysować wszelkie trójkąty: prostokątne, równoboczne, równoramienne, rozwarte, ostre.

import turtle

def trojkat(a, b, kat):
    pos = turtle.position() # zapamiętanie pierwszego wierzchołka

    turtle.forward(a)
    turtle.left(180 - kat)
    turtle.forward(b)

    turtle.goto(pos) # skok do pierwszego wierzchołka

    turtle.right(180 - kat) # przywrócenie pierwotnego kierunku głowy żółwia

trojkat(100, 100, 0)   # prosta
trojkat(100, 100, 30)
trojkat(100, 100, 60)  # równoboczny
trojkat(100, 100, 90)  # prostokątny
trojkat(100, 100, 120)
trojkat(100, 100, 150)
trojkat(100, 100, 180) # prosta
trojkat(100, 100, 210)
trojkat(100, 100, 240)
trojkat(100, 100, 270) # prostokątny
trojkat(100, 100, 300) # równoboczny
trojkat(100, 100, 330)
trojkat(100, 100, 360) # to samo co kont 0

trojkat(-100, 100, 0)   # prosta
trojkat(-100, 100, 30)
trojkat(-100, 100, 60)  # równoboczny
trojkat(-100, 100, 90)  # prostokątny
trojkat(-100, 100, 120)
trojkat(-100, 100, 150)
trojkat(-100, 100, 180) # prosta
trojkat(-100, 100, 210)
trojkat(-100, 100, 240)
trojkat(-100, 100, 270) # prostokątny
trojkat(-100, 100, 300) # równoboczny
trojkat(-100, 100, 330)
trojkat(-100, 100, 360) # to samo co kont 0

turtle.mainloop()

Kąty od 0 do 180, bok a dodatni.

Katy od 0 do 360, bok a dodatni.

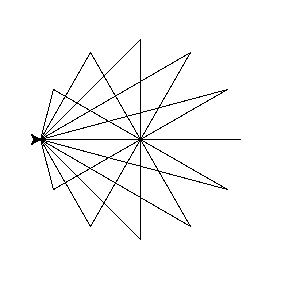
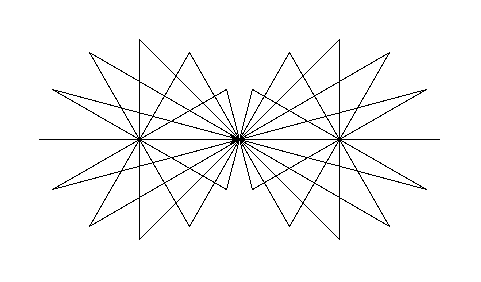
Katy od 0 do 360, bok a dodatni i ujemny.

Inne pomysły

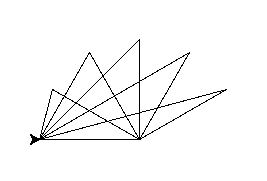
import turtle

# trojkat neony

def trojkat(a, b, kat):
    pos = turtle.position()
    turtle.forward(a)
    turtle.left(180-kat)
    turtle.forward(b)
    turtle.goto(pos)

    turtle.right(180-kat)

# trojkąty z lewej strony
for b in range(50, 301, 50):
    trojkat(300, b, 60)

# przejście na prawą stronę
turtle.forward(300)
turtle.left(180)

# trojkąty z prawej strony
# (kąt z minusem -60 aby rysować w drugą stronę)
for b in range(50, 301, 50):
    trojkat(300, b, -60)

turtle.mainloop()